| 数学中,线性代数这门课程的概念多、定理多、符号多、运算规律多、内容相互纵横交错,知识前后紧密联系。下面就对线代每章中一些具体知识点以及重要性质作一阐述:
一、行列式 行列式的核心内容是求行列式,包括具体行列式的计算和抽象行列式的计算,其中具体行列式的计算又有低阶和 二、矩阵 矩阵中除可逆阵、伴随阵、分块阵、初等阵等重要概念外,主要也是运算,其运算分两个层次,一是运用矩阵的性质对抽象矩阵进行运算,二是具体矩阵的数值运算。 下面的表格分类列出了逆矩阵
三、向量、线性方程组 向量与线性方程组的内容联系很密切,很多知识点相互之间都有或明或暗的相关性。复习这两章最有效的方法就是彻底弄清楚诸多知识点之间的内在联系,因为这样做首先能够保证做到真正意义上的理解,同时也是熟练掌握和灵活运用的前提。以下给出这部分主要知识点: 三个双重定义: 1.秩的定义 a.矩阵秩的定义:矩阵中非零子式的最高阶数。 b.向量组秩定义:向量组的极大线性无关组中的向量个数。 2.线性相关\无关的定义 a. 对于一组向量 b. 向量组 3.线性方程组的两种形式 a. 矩阵形式: b. 向量形式: 两条性质: 1.对于方阵 对于一般矩阵则有: 2.齐次线性方程组是否有非零解对应于系数矩阵的列向量组是否线性相关,而非齐次线性方程组是否有解对应于 以上两条性质可视为是将线性相关、行列式、秩、线性方程组几部分知识联系在一起的桥梁。 关于秩的一些结论:
四、特征值与特征向量 本章知识要点如下: 1.特征值和特征向量的定义及计算方法就是记牢一系列公式,如: 2.相似矩阵及其性质。定义式为 由以上定义可看出等价、合同、相似三者之间的关系:若与合同或相似则与必等价,反之不成立;合同与等价之间没有必然联系。 3.矩阵可相似对角化的条件。包括两个充要条件和两个充分条件,充要条件(1)是阶矩阵有个线性无关的特征向量;充要条件(2)是的任意 4.实对称矩阵极其相似对角化。阶实对称矩阵必可正交、相似于对角阵 五、二次型 将二次型表示成矩阵形式,用矩阵的方法研究二次型的问题主要有两个: 一是化二次型为标准形,这主要是正交变换法(这和实对称阵正交相似对角阵是一个问题的两种提法),在没有其他要求的情况下,用配方法得到标准形可能更方便些; 二是二次型的正定性问题,对具体的数值二次型,一般可用顺序主子式是否全部大于零来判别,而抽象的由给定矩阵的正定性,证明相关矩阵的正定性时,可利用标准形,规范形,特征值等到证明,这时应熟悉二次型正定有关的充分条件和必要条件。 |
| [发布者:] | ||
相关阅读:
·女硕士毕业后再度高考成为大专生(图)
·专科生考研心路:改写命运的只有自己
·硕博都为结婚愁:相亲会三成人全程戴面具
·你出国我考研:爱情正经受考验
·考研三战 我的悲情谁能懂?
|
 当前位置:
当前位置: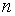 阶两种类型。主要方法是应用行列式按行或者列展开定理和化为上下三角行列式求解,还可能用到的方法包括:行列式的定义(
阶两种类型。主要方法是应用行列式按行或者列展开定理和化为上下三角行列式求解,还可能用到的方法包括:行列式的定义(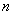 阶行列式的值为取自不同行、不同列的个元素的乘积的代数和)、性质
阶行列式的值为取自不同行、不同列的个元素的乘积的代数和)、性质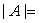
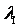
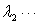
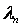 (其中
(其中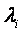 为矩阵
为矩阵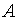 的特征值)、行列式的性质(如“数乘行列式等于用此数乘一行列式中的某一行或某一列”)。对于抽象行列式的求值,考点不在求行列式,而在于考虑
的特征值)、行列式的性质(如“数乘行列式等于用此数乘一行列式中的某一行或某一列”)。对于抽象行列式的求值,考点不在求行列式,而在于考虑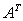 、
、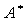 、
、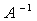 等的相关性质。
等的相关性质。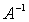 、伴随矩阵
、伴随矩阵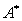 、矩阵转置的性质以供区别记忆:
、矩阵转置的性质以供区别记忆: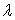 为矩阵
为矩阵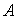 的特征值)
的特征值)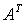
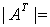
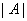
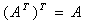
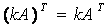
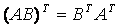
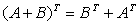
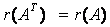
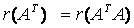
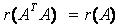
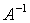
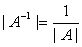
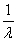
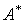
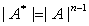
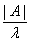
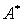 、
、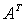 、三者之间有一个既好记又好用的性质
、三者之间有一个既好记又好用的性质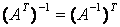
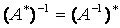
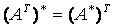
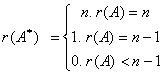
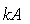 、矩阵之积
、矩阵之积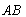 及矩阵之和
及矩阵之和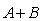
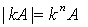
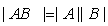
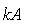 有特征值
有特征值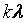
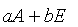 有特征值
有特征值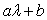
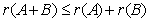
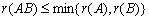
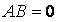 则有:
则有: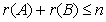
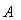 是可逆矩阵则有
是可逆矩阵则有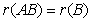 ;同样,若
;同样,若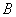 可逆则有
可逆则有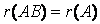
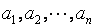 ,若存在不全为零的数
,若存在不全为零的数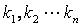 使得
使得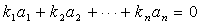 成立,则相量组线性相关,否则向量组线性无关,即上述等式当且仅当
成立,则相量组线性相关,否则向量组线性无关,即上述等式当且仅当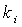 全为0时才成立。
全为0时才成立。 线性相关ó向量组中至少存在一个向量可由其余-1个向量线性表出;线性无关ó向量组中没有一个向量可由其余的向量线性表出。
线性相关ó向量组中至少存在一个向量可由其余-1个向量线性表出;线性无关ó向量组中没有一个向量可由其余的向量线性表出。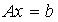
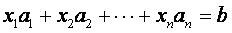
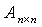 有:方阵
有:方阵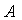 可逆ó存在方阵
可逆ó存在方阵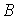 使得
使得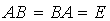 ó
ó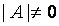 ó的行\列向量组均线性无关ó
ó的行\列向量组均线性无关ó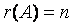 ó
ó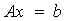 可由克莱姆法则判断有唯一解,而
可由克莱姆法则判断有唯一解,而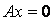 仅有零解。
仅有零解。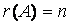 ó的列向量组线性无关ó仅有零解,
ó的列向量组线性无关ó仅有零解,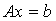 有唯一解。
有唯一解。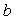 是否可以由的列向量组线性表出。
是否可以由的列向量组线性表出。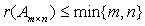 ;
;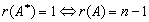 ;
;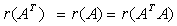 ;
;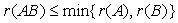 ;
;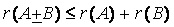 ;若有
;若有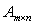 、
、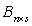 满足
满足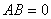 ,则
,则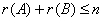 ;若
;若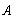 是可逆矩阵,则有
是可逆矩阵,则有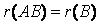 ;同样若
;同样若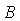 可逆则有
可逆则有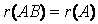 。非齐次线性方程组
。非齐次线性方程组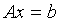 有唯一解则对应齐次方程组
有唯一解则对应齐次方程组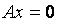 仅有零解,若
仅有零解,若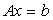 有无穷多解则有非零解;若有两个不同的解则有非零解;若是
有无穷多解则有非零解;若有两个不同的解则有非零解;若是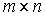 矩阵而
矩阵而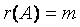 则
则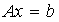 一定有解,而且当
一定有解,而且当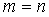 时是唯一解,当
时是唯一解,当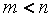 时是无穷多解,而若
时是无穷多解,而若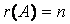 则
则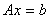 没有解或有唯一解。
没有解或有唯一解。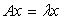
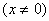 、
、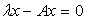 、
、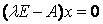 和
和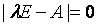 。在历年真题中常用到下列性质:若
。在历年真题中常用到下列性质:若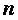 阶矩阵
阶矩阵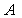 有个特征值
有个特征值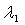
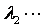
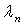 ,则有
,则有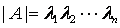 ;若矩阵有特征值
;若矩阵有特征值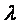 ,则
,则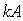 、
、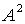 、
、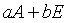 、
、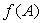 、、
、、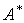 分别有特征值
分别有特征值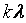 、
、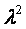 、
、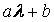 、
、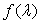 、
、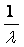 、
、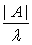 ,且对应特征向量等于
,且对应特征向量等于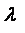 所对应的特征向量,而若
所对应的特征向量,而若 、
、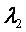 分别为矩阵、的特征值,则
分别为矩阵、的特征值,则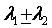 不一定为
不一定为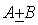 的特征值。
的特征值。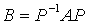 ,需要区分矩阵的相似、等价与合同:矩阵与矩阵等价的定义式是
,需要区分矩阵的相似、等价与合同:矩阵与矩阵等价的定义式是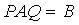 ,其中
,其中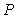 、
、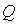 为可逆矩阵,此时矩阵可通过初等变换化为矩阵,并有
为可逆矩阵,此时矩阵可通过初等变换化为矩阵,并有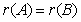 ;当
;当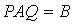 中的、
中的、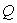 互逆时就变成了矩阵相似的定义式,即有
互逆时就变成了矩阵相似的定义式,即有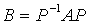 ,此时满足
,此时满足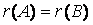 、
、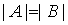 、
、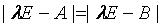 ,并且、有相同的特征值。矩阵合同的定义是
,并且、有相同的特征值。矩阵合同的定义是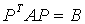 ,其中
,其中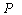 为可逆矩阵。
为可逆矩阵。 重特征根对应有个线性无关的特征向量;充分条件(1)是有个互不相同的特征值;充分条件(2)是为实对称矩阵。
重特征根对应有个线性无关的特征向量;充分条件(1)是有个互不相同的特征值;充分条件(2)是为实对称矩阵。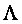 ,即有正交阵
,即有正交阵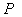 使得
使得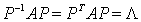 ,而且正交阵由对应的几个正交的特征向量组成。
,而且正交阵由对应的几个正交的特征向量组成。


















