极限篇 如何利用教材进行有效的复习,是大部分同学面临的主要问题。考研(论坛) 数学主要是对同学们“三基”的考查,因此复习数学的时候要抓住教材,好好利用教材。怎样才能更有效地利用教材进行复习,下面就如何来复习教材中的典型例题进行解读。 本文主要的目的:教会如何更有效地读懂例题、利用例题及模仿例题;学习如何来复习理解数学及解题方法。 注:本文以同济五版《高等数学》为蓝本。 极限 【求分式极限 (1)若 (2)若 (3)若, 求解分式极限时,首先要快速判断属于(1)(2)(3)哪种情况,对号入座,然后决定解决问题的方法及方式。 例1 (P58 例5)求 解:当
【解读】当时, 【注释1:说等价无穷小时,一定要标明是在哪种极限形式下的等价无穷小,这是因为等价无穷小是用极限来定义的;此处说的是“当 ~, 【注释2:看到此式,首先要想到要求必须记住的一个常用的等价无穷小代换公式
~, 【注释3:看到此式,首先要想到要求必须记住的一个常用的等价无穷小代换公式 所以
【注释4:此题完全用等价无穷小代换解决。当然也可以用Taylor公式进行求解,不过过程比较麻烦一些。此题为型未定式,若用罗比达法则会相当麻烦,不过大家可以尝试一下。】 【注释5:做完此题后,要掌握注释中的三个等价无穷小代换公式,做到熟练应用,最好能达到条件反射。】 例2 (P68 例8)求 解: 因为
利用定理3及极限的运算法则,便有
【解读】 因为 【注释1:上式的第一步是要凑出来重要极限,因此要对第二个重要极限的形式非常熟悉才行。第二个重要极限如下: 利用定理3及极限的运算法则,便有 【注释2:定理3表明当外函数连续时,极限号可以和外函数调换位置,这里的
【注释3:极限的运算法则指的是两个乘积函数的极限都存在时可以写成两个函数极限的乘积。即 【注释4:此题总的解题思路是:这是求幂指函数的极限,存在两种情况:一是用第二个重要极限,二是用换底公式。我们要熟练掌握这两种情况,特别是第二种情况,它的适用范围更广。】 【注释5:换底公式主要是针对类似于
例3 (P136 例10)求 解:
【解读】 【注释1:通过题目可以看出这是
【注释2:对上式应用罗比达法则而得。得到的仍然是型极限。】
【注释3:再次应用罗比达法则,这时发现
【注释4:此题给我们一个提示,在使用罗比达法则时,一定要先简化(变换或使用等价无穷小代换),以减少运算量。】 【注释5:此题另外的解法:直接使用等价无穷小代换即可,即由 |
| [发布者:] | ||
相关阅读:
·女硕士毕业后再度高考成为大专生(图)
·专科生考研心路:改写命运的只有自己
·硕博都为结婚愁:相亲会三成人全程戴面具
·你出国我考研:爱情正经受考验
·考研三战 我的悲情谁能懂?
|
 当前位置:
当前位置: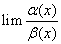 整体思路】共分为三种情况:(令
整体思路】共分为三种情况:(令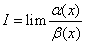 )
) 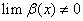 ,则有
,则有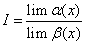 ;
;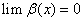 ,
,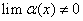 ,则有
,则有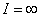 ;
;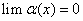 ,则属于
,则属于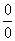 型未定式,则可用罗比达法则、等价无穷小代换等进行求解。
型未定式,则可用罗比达法则、等价无穷小代换等进行求解。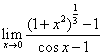
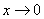 时,
时,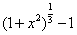 ~
~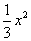 ,
,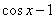 ~
~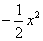 ,所以
,所以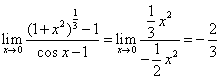
 时”。】
时”。】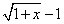 ~
~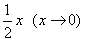 和
和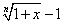 ~
~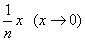 (此处也可以写成
(此处也可以写成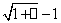 ~
~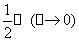 和
和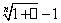 ~
~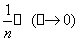 ),由此套用公式立即可以得到
),由此套用公式立即可以得到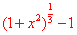 ~
~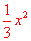 。】
。】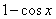 ~
~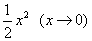 (此处也可以写成
(此处也可以写成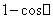 ~
~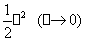 ),由此套用公式立即可以得到
),由此套用公式立即可以得到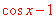 ~
~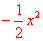 。】
。】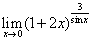
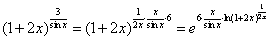
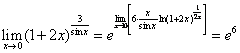
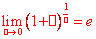 和
和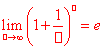 。之所以写成这样的形式,是让大家能明白,只要我们能凑成这两种标准形式之一就可以用这个公式,不用管□里是什么。最后一步应用的是换底公式,见注释4】
。之所以写成这样的形式,是让大家能明白,只要我们能凑成这两种标准形式之一就可以用这个公式,不用管□里是什么。最后一步应用的是换底公式,见注释4】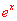 是外函数。】
是外函数。】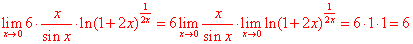 】
】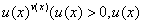 不恒等于
不恒等于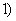 的幂指函数。对于这类函数可以采用以下方式进行求解:
的幂指函数。对于这类函数可以采用以下方式进行求解: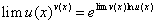 即转化成求
即转化成求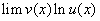 的极限。】
的极限。】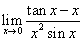
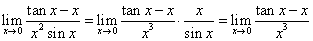
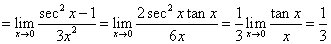
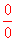 型极限,所以首先可以考虑用罗比达法则,但是由于分母比较复杂,求导不方便,所以需要进行变换一下再用罗比达法则】
型极限,所以首先可以考虑用罗比达法则,但是由于分母比较复杂,求导不方便,所以需要进行变换一下再用罗比达法则】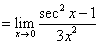
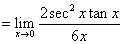
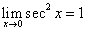 ,
,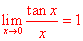 (注意这是重要极限
(注意这是重要极限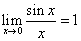 的一个变形,最好也要记住)。因此有】
的一个变形,最好也要记住)。因此有】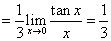
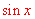 ~
~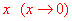 将分母变成
将分母变成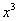 ,余下的步骤同上。】
,余下的步骤同上。】


















